research paper about standard deviation

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Standard deviation.

Samy El Omda ; Shane R. Sergent .

Affiliations

Last Update: August 14, 2023 .

• Definition/Introduction

The standard deviation (SD) measures the extent of scattering in a set of values, typically compared to the mean value of the set. [1] [2] [3]  The calculation of the SD depends on whether the dataset is a sample or the entire population. Ideally, studies would obtain data from the entire target population, which defines the population parameter. However, this is rarely possible in medical research, and hence a sample of the population is often used. [4]

The sample SD is determined through the following steps:

• Calculate the deviation of each observation from the mean
• Square each of these results
• Add these results together
• Divide this sum by the 'total number of observations minus 1' - the result at this stage is called the sample variance.
• Square root this result - This number will be the sample SD. [1]

For example, to work out the sample SD of the following data set: (4, 5, 5, 5, 7, 8, 8, 8, 9, 10)

The first step would be to calculate the mean of the data set. This is done by adding the value of each observation together and then dividing by the number of observations. The sum of the values would be 69, which then is divided by 10, so the mean would be 6.9. 

Then we would follow the same steps as above to work out the standard deviation:

• To calculate the deviation, subtract the mean from every observation which would result in the following values: (-2.9, -1.9, -1.9, -1.9, 0.1, 1.1, 1.1, 1.1, 2.1, 3.1)
• Then each value is squared to remove any negative values, resulting in the following values: (8.41, 3.61, 3.61, 3.61, 0.01, 1.21, 1.21, 1.21, 4.41, 9.61)
• The sum of these values is then calculated, which is 36.9
• The sample variance is then calculated. This is done by dividing the current value by the 'total number of observations minus 1', which in this case is 9: 36.9/9 = 4.1.
• Finally, the result is square rooted to find the sample standard deviation, which is 2.02 (to two decimal places).

The population SD is calculated similarly, with the only difference being in 'step 4' divided by the 'total number of observations' instead of ‘total number of observations minus 1’.

For example, if we take the same data set used above but instead calculate the SD assuming the data set was the total population.

• To calculate the deviation, subtract the mean from every observation which would result in the following values: (-2.9, -1.9, -1.9, -1.9, 0.1, 1.1, 1.1, 1.1, 2.1, 3.1)
• Then each value is squared to remove any negative values, resulting in the following values: (8.41, 3.61, 3.61, 3.61, 0.01, 1.21, 1.21, 1.21, 4.41, 9.61)
• The sum of these values is then calculated, which is 36.9
• The population variance is then calculated. This is done by dividing the current value by the 'total number of observations,' which in this case is 10. 36.9/10 = 3.69
• Finally, the result is square rooted to find the population standard deviation, which is 1.92 (to two decimal places)

As can be seen, by the formulas above, a large SD results from data with a large deviation from the mean, while a small SD shows the values are all quite close to the mean. [2] [5]

• Issues of Concern

Although the abovementioned method of calculating sample SD will always result in the correct value, as the data set increases in quantity, this method becomes increasingly burdensome. This is mainly due to having to calculate the difference from the mean of every value. This step can be bypassed through the following method:

• List the observed values of the data set in a column which we shall call 'x.'
• Find the 'sum of x' by adding all of the values in the column together.
• Square the value of the 'sum of x.'
• Divide this result by the 'total number of observations.' Call the result of this division 'y'.
• Square each value within the column 'x.'
• Find the sum of the above squares.
• Subtract the value 'y' from this sum.
• Divide this result by the 'total number of observations minus one' if calculating the sample SD. Divide this result by the 'total number of observations' if calculating the population SD.
• Finally, the result is square rooted to calculate the SD.

This method can quickly calculate the sample SD of a large data set, especially with a calculator with a memory function or an electronic data analysis program.

A mistake sometimes seen in research papers is whether the SD or the standard error of the mean (SEM) should be reported alongside the mean. The distinction between the SD and SEM is crucial but often overlooked. This results in authors reporting the incorrect one alongside their data. While the SD refers to the scatter of values around the sample mean, the SEM refers to the accuracy of the sample mean itself. This means the role of the SEM is to provide a measurement of the precision of the sample mean compared to the total population mean. Consequently, in contrast to the SD, the SEM does not provide information on the scatter of the sample. [5]

Despite this difference, the SEM is still often used in places where the SD should be stated. There have been many reasons hypothesized for this, such as a lack of full understanding of the meaning of these statistical concepts, leading authors to report what they have seen other authors report in their studies. This leads to multiple articles all publishing the SEM in an improper context. Another reason is that the SEM will be smaller than the SD and hence if presented alongside the mean, can give the impression that the data is more precise.

This incorrect impression would also be seen in the figures, as using the SEM will shorten the error bars. This can confuse even with experienced readers as the reader is expecting the SD to be paired with the mean and hence may incorrectly believe that the quoted SEM refers to the scatter of values around the mean (the SD). [5] [6]  In response to these issues, some journals only allow authors to present SDs and not SEMs to remove any chance of an author mistakenly using the SEM in an inappropriate context. [6] [7]

• Clinical Significance

Using SD allows for a quick overview of a population as long as the population follows a normal (Gaussian) distribution. In these populations, we know that 1 SD covers 68% of observations, 2 SD covers 95% of observations, and 3 SD covers 99.7% of observations. [5] [6] [8] [9]  This adds greater context to the mean value that is stated in many studies.

A hypothetical example will help clarify this point: Say a study looking at the effect of a new chemotherapy agent on life expectancy concludes that it increases life expectancy by 5 years.

A mean of 5 years could be achieved by widely different data sets. For example, everyone in the sample could have shown an increase between 4 to 6 years in life expectancy. However, another data set that would satisfy this mean would be if half the sample showed no statistical increase in life expectancy while the other half had an increase of 10 years. Including an SD can help readers quickly resolve this ambiguity as the former case would have a small SD while the latter would have a large SD. This allows readers to interpret the results of the study more accurately.

Furthermore, finding a “normal” range of measurements within medicine is often a key piece of information. One example would be the range of a laboratory value (such as full blood count) expected if the measurement was conducted in healthy individuals. Often this is the 95% reference range, where 2.5% of values will be lesser than the reference range, and 2.5% of values will be greater than the reference range. This makes the SD extremely useful in data sets that follow a normal distribution because it can quickly calculate the range in which 95% of values lie. [10]

Another advantage of reporting the SD is that it reports the scatter within the data in the same units as the data itself. This is in contrast to the variance of the data set, which is equivalent to the square of the SD, and hence its units are the units of the data squared. Therefore, although the variance can be useful in certain scenarios, it is generally not used in data description. Through sharing the same unit, the SD allows for the data to be more easily interpreted. [1] [2]

It is also important to know the disadvantages of using an SD. The main issue is in data sets where there are extreme values or severe skewness, as these results can influence the mean and SD by a significant amount. Consequently, in scenarios where the data set does not follow a normal (Gaussian) distribution, other measures of dispersion are often used. Most commonly, the interquartile range (IQR) is used alongside the median of the dataset. This is due to the IQR being significantly more resistant to extreme values, as when calculating the IQR, only the data between the first and third quartiles are factored in. The data between the first and third quartile represents the middle 50% of values, so any unusually high or low values will not affect the calculation of the IQR. This gives a more accurate picture of the data set’s distribution than the SD. [1] [11] [12] [13]

• Nursing, Allied Health, and Interprofessional Team Interventions

Evidence-based medicine plays a core role in patient care. It relies on integrating clinical expertise alongside the current best available literature. [14]  Consequently, keeping up to date with the current literature is key for all members of an interprofessional team to ensure they are acting in the best interest of a patient. To do this, all members must have a basic understanding of descriptive statistics (including the mean, median, mode, and standard deviation). Without this knowledge, it can be difficult to interpret the conclusions of research articles accurately.

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Samy El Omda declares no relevant financial relationships with ineligible companies.

Disclosure: Shane Sergent declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page El Omda S, Sergent SR. Standard Deviation. [Updated 2023 Aug 14]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• Understanding the Difference Between Standard Deviation and Standard Error of the Mean, and Knowing When to Use Which. [Indian J Psychol Med. 2020] Understanding the Difference Between Standard Deviation and Standard Error of the Mean, and Knowing When to Use Which. Andrade C. Indian J Psychol Med. 2020 Jul; 42(4):409-410. Epub 2020 Jul 20.
• Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. [Cochrane Database Syst Rev. 2022] Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. Crider K, Williams J, Qi YP, Gutman J, Yeung L, Mai C, Finkelstain J, Mehta S, Pons-Duran C, Menéndez C, et al. Cochrane Database Syst Rev. 2022 Feb 1; 2(2022). Epub 2022 Feb 1.
• Statistics Refresher for Molecular Imaging Technologists, Part 2: Accuracy of Interpretation, Significance, and Variance. [J Nucl Med Technol. 2018] Statistics Refresher for Molecular Imaging Technologists, Part 2: Accuracy of Interpretation, Significance, and Variance. Farrell MB. J Nucl Med Technol. 2018 Jun; 46(2):76-80. Epub 2018 Feb 2.
• Review Translational Metabolomics of Head Injury: Exploring Dysfunctional Cerebral Metabolism with Ex Vivo NMR Spectroscopy-Based Metabolite Quantification. [Brain Neurotrauma: Molecular, ...] Review Translational Metabolomics of Head Injury: Exploring Dysfunctional Cerebral Metabolism with Ex Vivo NMR Spectroscopy-Based Metabolite Quantification. Wolahan SM, Hirt D, Glenn TC. Brain Neurotrauma: Molecular, Neuropsychological, and Rehabilitation Aspects. 2015
• Review Standard deviation and standard error of the mean. [Korean J Anesthesiol. 2015] Review Standard deviation and standard error of the mean. Lee DK, In J, Lee S. Korean J Anesthesiol. 2015 Jun; 68(3):220-3. Epub 2015 May 28.

Recent Activity

• Standard Deviation - StatPearls Standard Deviation - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Standard deviation and standard error of the mean

Dong kyu lee, sangseok lee.

• Author information
• Article notes
• Copyright and License information

Corresponding author: Dong Kyu Lee, M.D., Ph.D. Department of Anesthesiology and Pain Medicine, Korea University Guro Hospital, 148, Gurodong-ro, Guro-gu, Seoul 152-703, Korea. Tel: 82-2-2626-3237, Fax: 82-2-2626-1437, [email protected]

Corresponding author.

Received 2015 Apr 2; Revised 2015 May 6; Accepted 2015 May 7; Issue date 2015 Jun.

This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License ( http://creativecommons.org/licenses/by-nc/4.0/ ), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

In most clinical and experimental studies, the standard deviation (SD) and the estimated standard error of the mean (SEM) are used to present the characteristics of sample data and to explain statistical analysis results. However, some authors occasionally muddle the distinctive usage between the SD and SEM in medical literature. Because the process of calculating the SD and SEM includes different statistical inferences, each of them has its own meaning. SD is the dispersion of data in a normal distribution. In other words, SD indicates how accurately the mean represents sample data. However the meaning of SEM includes statistical inference based on the sampling distribution. SEM is the SD of the theoretical distribution of the sample means (the sampling distribution). While either SD or SEM can be applied to describe data and statistical results, one should be aware of reasonable methods with which to use SD and SEM. We aim to elucidate the distinctions between SD and SEM and to provide proper usage guidelines for both, which summarize data and describe statistical results.

Keywords: Standard deviation, Standard error of the mean

A data is said to follow a normal distribution when the values of the data are dispersed evenly around one representative value. A normal distribution is a prerequisite for a parametric statistical analysis [ 1 ]. The mean in a normally distributed data represents the central tendency of the values of the data. However, the mean alone is not sufficient when attempting to explain the shape of the distribution; therefore, many medical literatures employ the standard deviation (SD) and the standard error of the mean (SEM) along with the mean to report statistical analysis results [ 2 ].

The objective of this article is to state the differences with regard to the use of the SD and SEM, which are used in descriptive and statistical analysis of normally distributed data, and to propose a standard against which statistical analysis results in medial literatures can be evaluated.

Medical studies begin by establishing a hypothesis about a population and extracting a sample from the population to test the hypothesis. The extracted sample will take a normal distribution if the sampling process was conducted via an appropriate randomization method with a sufficient sample size . As with all normally distributed data, the characteristics of the sample are represented by the mean , variance or SD. The variance or SD includes the differences of the observed values from the mean ( Fig. 1 ); thus, these values represent the variation of the data [ 1 , 2 , 3 ]. For instance, if the observed values are scattered closely around the mean value, the variance - as well as the SD - are reduced. However, the variance can confuse the interpretation of the data because it is computed by squaring the units of the observed values. Hence, the SD, which uses the same units used with the mean , is more appropriate [ 3 ] (Equations 1 and 2).

Fig. 1. Process of data description. First, we gather raw data from the population by means of randomization (A). We then arrange the each value according to the scale (frequency distribution); we can presume the shape of the distribution (probability distribution) and can calculate the mean and standard deviation (B). Using these mean and standard deviation, we produce a model of the normal distribution (C). This distribution represents the characteristics of the data we gathered and is the normal distribution, with which statistical inferences can be made (χ̅: mean, SD: standard deviation, χ i : observation value, n: sample size).

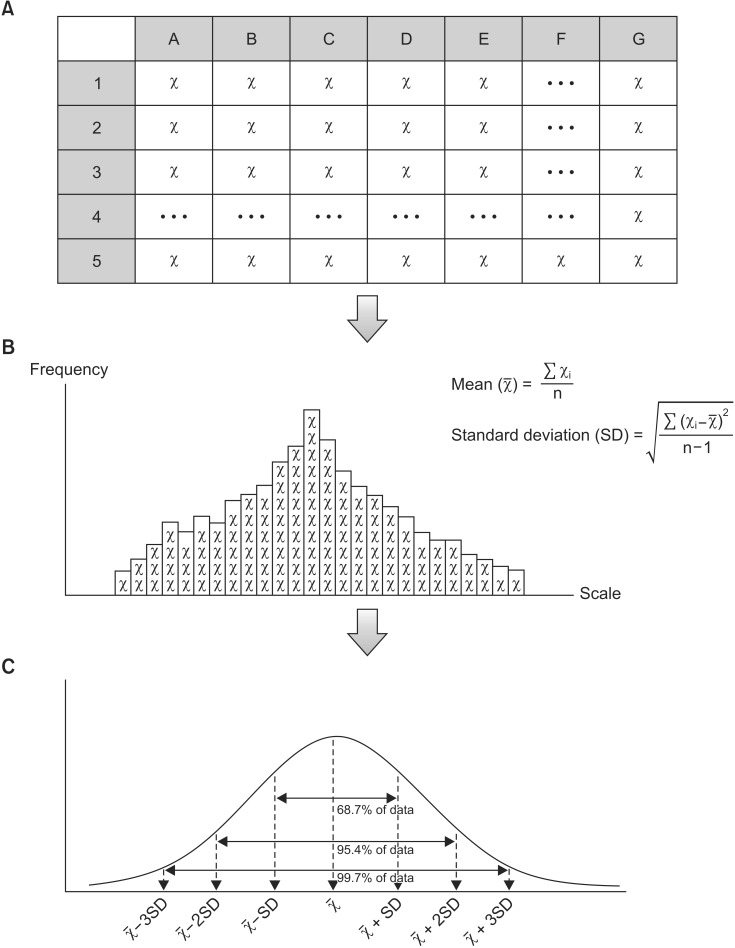
As mentioned previously, using the SD concurrently with the mean can more accurately estimate the variation in a normally distributed data. In other words, a normally distributed statistical model can be achieved by examining the mean and the SD of the data [ 1 ] ( Fig. 1 , Equations 1 and 2). In such models, approximately 68.7% of the observed values are placed within one SD from the mean , approximately 95.4% of the observed values are arranged within two SDs from the mean , and about 99.7% of the observed values are positioned within three SDs from the mean [ 1 , 4 ]. For this reason, most medical literatures report their samples in the form of the mean and SD [ 5 ].

The sample as referred to in medical literature is a set of observed values from a population . An experiment must be conducted on the entire population to acquire a more accurate confirmation of a hypothesis, but it is essentially impossible to survey an entire population . As a result, an appropriate sampling process - a process of extracting a sample that represents the characteristics of a population - is essential to acquire reliable results. For this purpose, an appropriate sample size is determined during the research planning stage and the sampling is done via a randomization method . Nevertheless, the extracted sample is still a part of the population ; thus, the sample mean is an estimated value of the population mean . When the samples of the same sample size are repeatedly and randomly taken from the same population , they are different each other because of sampling variation as well as sample means ( Fig. 2 , Level B). The distribution of different sample means , which is achieved via repeated sampling processes, is referred to as the sampling distribution and it takes a normal distribution pattern ( Fig. 2 , Level C) [ 1 , 6 , 7 ]. Therefore, the SD of the sampling distribution can be computed; this value is referred to as the SEM [ 1 , 6 , 7 ]. The SEM is dependent on the variation in the population and the number of the extracted samples. A large variation in the population causes a large difference in the sample means , ultimately resulting in a larger SEM. However, as more samples are extracted from the population , the sample means move closer to the population mean , which results in a smaller SEM. In short, the SEM is an indicator of how close the sample mean is to the population mean [ 7 ]. In reality, however, only one sample is extracted from the population . Therefore, the SEM is estimated using the SD and a sample size (Estimated SEM). The SEM computed by a statistical program is an estimated value calculated via this process [ 5 ] (Equation 3).

Fig. 2. Process of statistical inference. Level A indicates the population. In most experiments, we only obtain one set of sample data from the population using randomization (Level B); the mean and standard deviation are calculated from sample data we have. For statistical inference purposes, we assume that there are several sample data sets from the population (Level B); the means of each sample data set produce the sampling distribution (Level C). Using this sampling distribution, statistical analysis can be conducted. In this situation, the estimated standard error of the mean or the 95% confidence interval has an important role during the statistical analysis process (χ̅: mean, SD: standard deviation, n: sample size, N: number of sample data sets extracted from population).

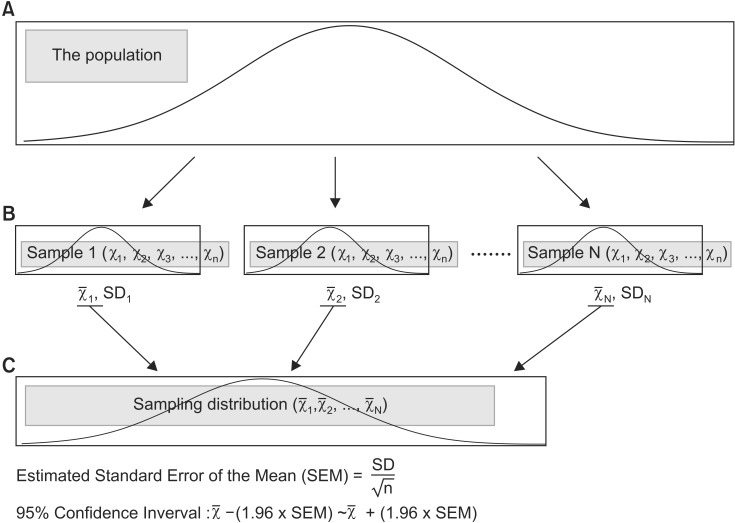
A confidence interval is set to illustrate the population mean intuitively. A 95% confidence interval is the most common [ 3 , 7 ]. The SEM of a sampling distribution is estimated from one sample, and a confidence interval is determined from the SEM ( Fig. 2 , Level C). In the strict sense, the 95% confidence interval provides the information about a range within which the 95% sample means will fall, it is not a range for the population mean with 95% confidence. For example, a 95% confidence interval signifies that when 100 sample means are calculated from 100 samples from a population , 95 of them are included within the said confidence interval and 5 are placed outside of the confidence interval . In other words, it does not mean that there is a 95% probability that the population mean lies within the 95% confidence interval .

When statistically comparing data sets, researchers estimate the population of each sample and examine whether they are identical. The SEM - not the SD, which represents the variation in the sample - is used to estimate the population mean ( Fig. 2 ) [ 4 , 8 , 9 ]. Via this process, researchers conclude that the sample used in their studies appropriately represents the population within the error range specified by the pre-set significance level [ 4 , 6 , 8 ].

The SEM is smaller than the SD, as the SEM is estimated usually the SD divided by the square root of the sample size (Equations 2 and 3). For this reason, researchers are tempted to use the SEM when describing their samples. It is acceptable to use either the SEM or SD to compare two different groups if the sample sizes of the two groups are equal; however, the sample size must be stated in order to deliver accurate information. For example, when a population has a large amount of variation, the SD of an extracted sample from this population must be large. However, the SEM will be small if the sample size is deliberately increased. In such cases, it would be easy to misinterpret the population from using the SEM in descriptive statistics . Such cases are common in medical research, because the variables in medical research impose many possible biases originated from inter- and intra-individual variations originated from underlying general conditions of the patients and so on. When interpreting the SD and SEM, however, the exact meaning and purposes of the SD and SEM should be considered to deliver correct information. [ 3 , 4 , 6 , 7 , 10 ].

We examined 36 clinical or experimental studies published in Volume 6, Numbers 1 through 6 of the Korean Journal of Anesthesiology and found that a few of the studies inappropriately used the SD and SEM. First, examining the descriptive statistics , we found that all of the studies used the mean and SD or the observed number and percentage. One study suggested a 95% confidence interval ; this particular study appropriately stated the sample size along the confidence interval , offering a clearer understanding of the data suggested in the study [ 11 ]. Among the 36 studies examined, only one study described the results of a normality test [ 12 ]. Second, all 36 studies used the SD, the observed number or the percentage to describe their statistical results. One study did not specify what the values in the graphs and tables represent (i.e., the mean , SD or interquartile range ). There was also a study that used the mean in the text but showed an interquartile range in the graphs. Sixteen studies used either the observed number or the percentage, and most of them reported their results without a confidence interval . Only two studies stated confidence intervals , but only one of those two studies appropriately used the confidence interval [ 13 ]. As shown above, we found that some of the studies have inappropriately used the SD, SEM and confidence intervals in reporting their statistical results. Such instances of the inappropriate use of statistics must be meticulously screened during manuscript reviews and evaluations because they may hamper an accurate comprehension of a study's data.

In conclusion, the SD reflects the variation in a normally distributed data, and the SEM represents the variation in the sample means of a sampling distribution . With this in mind, it is pertinent to use the SD (paired with a normality test ) to describe the characteristics of a sample; however, the SEM or confidence interval can be used for the same purpose if the sample size is specified. The SEM, paired with the sample size , is more useful when reporting statistical results because it allows an intuitive comparison between the estimated populations via graphs or tables.

• 1. Curran-Everett D, Taylor S, Kafadar K. Fundamental concepts in statistics: elucidation and illustration. J Appl Physiol (1985) 1998;85:775–786. doi: 10.1152/jappl.1998.85.3.775. [ DOI ] [ PubMed ] [ Google Scholar ]
• 2. Curran-Everett D, Benos DJ. Guidelines for reporting statistics in journals published by the American Physiological Society: the sequel. Adv Physiol Educ. 2007;31:295–298. doi: 10.1152/advan.00022.2007. [ DOI ] [ PubMed ] [ Google Scholar ]
• 3. Altman DG, Bland JM. Standard deviations and standard errors. BMJ. 2005;331:903. doi: 10.1136/bmj.331.7521.903. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 4. Carlin JB, Doyle LW. Statistics for clinicians: 4: Basic concepts of statistical reasoning: hypothesis tests and the t-test. J Paediatr Child Health. 2001;37:72–77. doi: 10.1046/j.1440-1754.2001.00634.x. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Livingston EH. The mean and standard deviation: what does it all mean? J Surg Res. 2004;119:117–123. doi: 10.1016/j.jss.2004.02.008. [ DOI ] [ PubMed ] [ Google Scholar ]
• 6. Rosenbaum SH. Statistical methods in anesthesia. In: Miller RD, Cohen NH, Eriksson LI, Fleisher LA, Wiener-Kronish JP, Young WL, editors. Miller's Anesthesia. 8th ed. Philadelphia: Elsevier Inc; 2015. pp. 3247–3250. [ Google Scholar ]
• 7. Curran-Everett D. Explorations in statistics: standard deviations and standard errors. Adv Physiol Educ. 2008;32:203–208. doi: 10.1152/advan.90123.2008. [ DOI ] [ PubMed ] [ Google Scholar ]
• 8. Carley S, Lecky F. Statistical consideration for research. Emerg Med J. 2003;20:258–262. doi: 10.1136/emj.20.3.258. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 9. Mahler DL. Elementary statistics for the anesthesiologist. Anesthesiology. 1967;28:749–759. [ PubMed ] [ Google Scholar ]
• 10. Nagele P. Misuse of standard error of the mean (SEM) when reporting variability of a sample. A critical evaluation of four anaesthesia journals. Br J Anaesth. 2003;90:514–516. doi: 10.1093/bja/aeg087. [ DOI ] [ PubMed ] [ Google Scholar ]
• 11. Koh MJ, Park SY, Park EJ, Park SH, Jeon HR, Kim MG, et al. The effect of education on decreasing the prevalence and severity of neck and shoulder pain: a longitudinal study in Korean male adolescents. Korean J Anesthesiol. 2014;67:198–204. doi: 10.4097/kjae.2014.67.3.198. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 12. Kim HS, Lee DC, Lee MG, Son WR, Kim YB. Effect of pneumoperitoneum on the recovery from intense neuromuscular blockade by rocuronium in healthy patients undergoing laparoscopic surgery. Korean J Anesthesiol. 2014;67:20–25. doi: 10.4097/kjae.2014.67.1.20. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 13. Lee H, Shon YJ, Kim H, Paik H, Park HP. Validation of the APACHE IV model and its comparison with the APACHE II, SAPS 3, and Korean SAPS 3 models for the prediction of hospital mortality in a Korean surgical intensive care unit. Korean J Anesthesiol. 2014;67:115–122. doi: 10.4097/kjae.2014.67.2.115. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (626.2 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

•  We're Hiring!
•  Help Center

Standard Deviation

• Most Cited Papers
• Most Downloaded Papers
• Newest Papers
• Last »
• Workspaces Follow Following
• Electronic transactions Follow Following
• Transfer Function Follow Following
• Biomedical Signal Processing Follow Following
• Statistical Significance Follow Following
• Frequency Follow Following
• Recall Follow Following
• Helically Coil Heat Exchanger Follow Following
• Attenuation Follow Following
• Electronic Government Follow Following

Enter the email address you signed up with and we'll email you a reset link.

• Academia.edu Journals
•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

• Research article
• Open access
• Published: 19 December 2014

Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range

• Xiang Wan 1 ,
• Wenqian Wang 2 ,
• Jiming Liu 1 &
• Tiejun Tong 3  

BMC Medical Research Methodology volume  14 , Article number:  135 ( 2014 ) Cite this article

218k Accesses

6213 Citations

60 Altmetric

Metrics details

In systematic reviews and meta-analysis, researchers often pool the results of the sample mean and standard deviation from a set of similar clinical trials. A number of the trials, however, reported the study using the median, the minimum and maximum values, and/or the first and third quartiles. Hence, in order to combine results, one may have to estimate the sample mean and standard deviation for such trials.

In this paper, we propose to improve the existing literature in several directions. First, we show that the sample standard deviation estimation in Hozo et al.’s method (BMC Med Res Methodol 5:13, 2005) has some serious limitations and is always less satisfactory in practice. Inspired by this, we propose a new estimation method by incorporating the sample size. Second, we systematically study the sample mean and standard deviation estimation problem under several other interesting settings where the interquartile range is also available for the trials.

We demonstrate the performance of the proposed methods through simulation studies for the three frequently encountered scenarios, respectively. For the first two scenarios, our method greatly improves existing methods and provides a nearly unbiased estimate of the true sample standard deviation for normal data and a slightly biased estimate for skewed data. For the third scenario, our method still performs very well for both normal data and skewed data. Furthermore, we compare the estimators of the sample mean and standard deviation under all three scenarios and present some suggestions on which scenario is preferred in real-world applications.

Conclusions

In this paper, we discuss different approximation methods in the estimation of the sample mean and standard deviation and propose some new estimation methods to improve the existing literature. We conclude our work with a summary table (an Excel spread sheet including all formulas) that serves as a comprehensive guidance for performing meta-analysis in different situations.

Peer Review reports

In medical research, it is common to find that several similar trials are conducted to verify the clinical effectiveness of a certain treatment. While individual trial study could fail to show a statistically significant treatment effect, systematic reviews and meta-analysis of combined results might reveal the potential benefits of treatment. For instance, Antman et al. [ 1 ] pointed out that systematic reviews and meta-analysis of randomized control trials would have led to earlier recognition of the benefits of thrombolytic therapy for myocardial infarction and may save a large number of patients.

Prior to the 1990s, the traditional approach to combining results from multiple trials is to conduct narrative (unsystematic) reviews, which are mainly based on the experience and subjectivity of experts in the area [ 2 ]. However, this approach suffers from many critical flaws. The major one is due to inconsistent criteria of different reviewers. To claim a treatment effect, different reviewers may use different thresholds, which often lead to opposite conclusions from the same study. Hence, from the mid-1980s, systematic reviews and meta-analysis have become an imperative tool in medical effectiveness measurement. Systematic reviews use specific and explicit criteria to identify and assemble related studies and usually provide a quantitative (statistic) estimate of aggregate effect over all the included studies. The methodology in systematic reviews is usually referred to as meta-analysis. With the combination of several studies and more data taken into consideration in systematic reviews, the accuracy of estimations will get improved and more precise interpretations towards the treatment effect can be achieved via meta-analysis.

In meta-analysis of continuous outcomes, the sample size, mean, and standard deviation are required from included studies. This, however, can be difficult because results from different studies are often presented in different and non-consistent forms. Specifically in medical research, instead of reporting the sample mean and standard deviation of the trials, some trial studies only report the median, the minimum and maximum values, and/or the first and third quartiles. Therefore, we need to estimate the sample mean and standard deviation from these quantities so that we can pool results in a consistent format. Hozo et al. [ 3 ] were the first to address this estimation problem. They proposed a simple method for estimating the sample mean and the sample variance (or equivalently the sample standard deviation) from the median, range, and the size of the sample. Their method is now widely accepted in the literature of systematic reviews and meta-analysis. For instance, a search of Google Scholar on November 12, 2014 showed that the article of Hozo et al.’s method has been cited 722 times where 426 citations are made recently in 2013 and 2014.

In this paper, we will show that the estimation of the sample standard deviation in Hozo et al.’s method has some serious limitations. In particular, their estimator did not incorporate the information of the sample size and so consequently, it is always less satisfactory in practice. Inspired by this, we propose a new estimation method that will greatly improve their method. In addition, we will investigate the estimation problem under several other interesting settings where the first and third quartiles are also available for the trials.

Throughout the paper, we define the following summary statistics:

a = the minimum value,

q 1 = the first quartile,

m = the median,

q 3 = the third quartile,

b = the maximum value,

n = the sample size.

The { a , q 1 , m , q 3 , b } is often referred to as the 5-number summary [ 4 ]. Note that the 5-number summary may not always be given in full. The three frequently encountered scenarios are:

Hozo et al.’s method only addressed the estimation of the sample mean and variance under Scenario C 1 while Scenarios C 2 and C 3 are also common in systematic review and meta-analysis. In Sections 'Methods’ and 'Results’, we study the estimation problem under these three scenarios, respectively. Simulation studies are conducted in each scenario to demonstrate the superiority of the proposed methods. We conclude the paper in Section 'Discussion’ with some discussions and a summary table to provide a comprehensive guidance for performing meta-analysis in different situations.

Estimating X ̄ and S from C 1

Scenario C 1 assumes that the median, the minimum, the maximum and the sample size are given for a clinical trial study. This is the same assumption as made in Hozo et al.’s method. To estimate the sample mean and standard deviation, we first review the Hozo et al.’s method and point out some limitations of their method in estimating the sample standard deviation. We then propose to improve their estimation by incorporating the information of the sample size.

Throughout the paper, we let X 1 , X 2 ,…, X n be a random sample of size n from the normal distribution N ( μ , σ 2 ), and X (1) ≤ X (2) ≤ ⋯ ≤ X ( n ) be the ordered statistics of X 1 , X 2 , ⋯ , X n . Also for the sake of simplicity, we assume that n = 4 Q + 1 with Q being a positive integer. Then

In this section, we are interested in estimating the sample mean X ̄ = ∑ i = 1 n X i and the sample standard deviation S = ∑ i = 1 n ( X i - X ̄ ) 2 / ( n - 1 ) 1 / 2 , given that a , m , b , and n of the data are known.

Hozo et al.’s method

For ease of notation, let M = 2 Q + 1. Then, M = ( n + 1)/2. To estimate the mean value, Hozo et al. applied the following inequalities:

Adding up all above inequalities and dividing by n , we have LB 1 ≤ X ̄ ≤ UB 1 , where the lower and upper bounds are

Hozo et al. then estimated the sample mean by

Note that the second term in (2) is negligible when the sample size is large. A simplified mean estimation is given as

For estimating the sample standard deviation, by assuming that the data are non-negative, Hozo et al. applied the following inequalities:

With some simple algebra and approximations on the formula (4), we have LSB 1 ≤ ∑ i = 1 n X i 2 ≤ USB 1 , where the lower and upper bounds are

Then by (3) and the approximation ∑ i = 1 n X i 2 ≈ ( LSB 1 + USB 1 ) / 2 , the sample standard deviation is estimated by S = S 2 , where

When n is large, it results in the following well-known range rule of thumb:

Note that the range rule of thumb (5) is independent of the sample size. It may not work well in practice, especially when n is extremely small or large. To overcome this problem, Hozo et al. proposed the following improved range rule of thumb with respect to the different size of the sample:

where the formula for n ≤ 15 is derived under the equidistantly spaced data assumption, and the formula for n > 70 is suggested by the Chebyshev’s inequality [ 5 ]. Note also that when the data are symmetric, we have a + b ≈ 2 m and so

Hozo et al. showed that the adaptive formula (6) performs better than the original formula (5) in most settings.

Improved estimation of S

We think, however, that the adaptive formula (6) may still be less accurate for practical use. First, the threshold values 15 and 70 are suggested somewhat arbitrarily. Second, given the normal data N ( μ , σ 2 ) with σ > 0 being a finite value, we know that σ ≈ ( b - a )/6 → ∞ as n → ∞ . This contradicts to the assumption that σ is a finite value. Third, the non-negative data assumption in Hozo et al.’s method is also quite restrictive.

In this section, we propose a new estimator to further improve (6) and, in addition, we remove the non-negative assumption on the data. Let Z 1 ,…, Z n be independent and identically distributed (i.i.d.) random variables from the standard normal distribution N (0,1), and Z (1) ≤ ⋯ ≤ Z ( n ) be the ordered statistics of Z 1 ,…, Z n . Then X i = μ + σ Z i and X ( i ) = μ + σ Z ( i ) for i = 1,…, n . In particular, we have a = μ + σ Z (1) and b = μ + σ Z ( n ) . Since E ( Z (1) ) = - E ( Z ( n ) ), we have E ( b - a ) = 2 σ E ( Z ( n ) ). Hence, by letting ξ ( n ) = 2 E ( Z ( n ) ), we choose the following estimation for the sample standard deviation:

Note that ξ ( n ) plays an important role in the sample standard deviation estimation. If we let ξ ( n ) ≡ 4, then (7) reduces to the original rule of thumb in (5). If we let ξ ( n ) = 12 for n ≤ 15, 4 for 15 < n ≤ 70, or 6 for n > 70, then (7) reduces to the improved rule of thumb (6).

Next, we present a method to approximate ξ ( n ) and establish an adaptive rule of thumb for standard deviation estimation. By David and Nagaraja’s method [ 6 ], the expected value of Z ( n ) is

where ϕ ( z ) = 1 2 π e - z 2 / 2 is the probability density function and Φ ( z ) = ∫ - ∞ z ϕ ( t ) dt is the cumulative distribution function of the standard normal distribution. For ease of reference, we have computed the values of ξ ( n ) by numerical integration using the computer in Table  1 for n up to 50. From Table  1 , it is evident that the adaptive formula (6) in Hozo et al.’s method is less accurate and also less flexible.

When n is large (say n > 50), we can apply Blom’s method [ 7 ] to approximate E ( Z ( n ) ). Specifically, Blom suggested the following approximation for the expected values of the order statistics:

where Φ -1 ( z ) is the inverse function of Φ ( z ), or equivalently, the upper z th percentile of the standard normal distribution. Blom observed that the value of α increases as n increases, with the lowest value being 0.330 for n = 2. Overall, Blom suggested α = 0.375 as a compromise value for practical use. Further discussion on the choice of α can be seen, for example, in [ 8 ] and [ 9 ]. Finally, by (7) and (8) with r = n and α = 0.375, we estimate the sample standard deviation by

In the statistical software R, the upper z th percentile Φ -1 ( z ) can be computed by the command “qnorm( z )”.

Estimating X ̄ and S from C 2

Scenario C 2 assumes that the first quartile, q 1 , and the third quartile, q 3 , are also available in addition to C 1 . In this setting, Bland’s method [ 10 ] extended Hozo et al.’s results by incorporating the additional information of the interquartile range (IQR). He further claimed that the new estimators for the sample mean and standard deviation are superior to those in Hozo et al.’s method. In this section, we first review the Bland’s method and point out some limitations of this method. We then, accordingly, propose to improve this method by incorporating the size of a sample.

Bland’s method

Noting that n = 4 Q + 1, we have Q = ( n - 1)/4. To estimate the sample mean, Bland’s method considered the following inequalities:

Adding up all above inequalities and dividing by n , it results in LB 2 ≤ X ̄ ≤ UB 2 , where the lower and upper bounds are

Bland then estimated the sample mean by ( LB 2 + UB 2 )/2. When the sample size is large, by ignoring the negligible second terms in LB 2 and UB 2 , a simplified mean estimation is given as

For the sample standard deviation, Bland considered some similar inequalities as in (4). Then with some simple algebra and approximation, it results in LSB 2 ≤ ∑ i = 1 n X i 2 ≤ USB 2 , where the lower and upper bounds are

Next, by the approximation ∑ i = 1 n X i 2 ≈ ( LSB 2 + USB 2 ) / 2 ,

Bland’s method then took the square root S 2 to estimate the sample standard deviation. Note that the estimator (11) is independent of the sample size n . Hence, it may not be sufficient for general use, especially when n is small or large. In the next section, we propose an improved estimation for the sample standard deviation by incorporating the additional information of the sample size.

Recall that the range b - a was used to estimate the sample standard deviation in Scenario C 1 . Now for Scenario C 2 , since the IQR q 3 - q 1 is also known, another approach is to estimate the sample standard deviation by ( q 3 - q 1 )/ η ( n ), where η ( n ) is a function of n . Taking both methods into account, we propose the following combined estimator for the sample standard deviation:

Following Section 'Improved estimation of S ’, we have ξ ( n ) = 2 E ( Z ( n ) ). Now we look for an expression for η ( n ) so that ( q 3 - q 1 )/ η ( n ) also provides a good estimate of S . By (1), we have q 1 = μ + σ Z ( Q +1) and q 3 = μ + σ Z (3 Q +1) . Then, q 3 - q 1 = σ ( Z (3 Q +1) - Z ( Q +1) ). Further, by noting that E ( Z ( Q +1) ) = - E ( Z (3 Q +1) ), we have E ( q 3 - q 1 ) = 2 σ E ( Z (3 Q +1) ). This suggests that

In what follows, we propose a method to compute the value of η ( n ). By [ 6 ], the expected value of Z (3 Q +1) is

In Table  2 , we provide the numerical values of η ( n ) = 2 E ( Z (3 Q +1) ) for Q ≤ 50 using the statistical software R. When n is large, we suggest to apply the formula (8) to approximate η ( n ). Specifically, noting that Q = ( n - 1)/4, we have η ( n ) ≈ 2 Φ -1 ((0.75 n - 0.125)/( n + 0.25)) for r = 3 Q + 1 with α = 0.375. Then consequently, for the scenario C 2 we estimate the sample standard deviation by

We note that the formula (13) is more concise than the formula (11). The numerical comparison between the two formulas will be given in the section of simulation study.

Estimating X ̄ and S from C 3

Scenario C 3 is an alternative way to report the study other than Scenarios C 1 and C 2 . It reports the first and third quartiles instead of the minimum and maximum values. One main reason to report C 3 is because the IQR is usually less sensitive to outliers compared to the range. For the new scenario, we note that Hozo et al.’s method and Bland’s method will no longer be applicable. Particularly, if their ideas are followed, we have the following inequalities:

where the first Q inequalities are unbounded for the lower limit, and the last Q inequalities are unbounded for the upper limit. Now adding up all above inequalities and dividing by n , we have - ∞ ≤ X ̄ ≤ ∞ . This shows that the approaches based on the inequalities do not apply to Scenario C 3 .

In contrast, the following procedure is commonly adopted in the recent literature including [ 11 , 12 ]: “ If the study provided medians and IQR, we imputed the means and standard deviations as described by Hozo et al. [ [ 3 ] ]. We calculated the lower and upper ends of the range by multiplying the difference between the median and upper and lower ends of the IQR by 2 and adding or subtracting the product from the median, respectively ”. This procedure, however, performs very poorly in our simulations (not shown).

A quantile method for estimating X ̄ and S

In this section, we propose a quantile method for estimating the sample mean and the sample standard deviation, respectively. In detail, we first revisit the estimation method in Scenario C 2 . By (10), we have

Now for Scenario C 3 , a and b are not given. Hence, a reasonable solution is to remove a and b from the estimation and keep the second term. By doing so, we have the estimation form as X ̄ ≈ ( q 1 + m + q 3 ) / C , where C is a constant. Finally, noting that E ( q 1 + m + q 3 ) = 3 μ + σ E ( Z ( Q +1) + Z 2 Q +1 + Z (3 Q +1) ) = 3 μ , we let C = 3 and define the estimator of the sample mean as follows:

For the sample standard deviation, following the idea in constructing (12) we propose the following estimation:

where η ( n ) = 2 E ( Z (3 Q +1) ). As mentioned above that E ( q 3 - q 1 ) = 2 σ E ( Z (3 Q +1) ) = σ η ( n ), therefore, the estimator (15) provides a good estimate for the sample standard deviation. The numerical values of η ( n ) are given in Table  2 for Q ≤ 50. When n is large, by the approximation E ( Z (3 Q +1) ) ≈ Φ -1 ((0.75 n - 0.125)/( n + 0.25)), we can also estimate the sample standard deviation by

A similar estimator for estimating the standard deviation from IQR is provided in the Cochrane Handbook [ 13 ], which is defined as

Note that the estimator (17) is also independent of the sample size n and thus may not be sufficient for general use. As we can see from Table  2 , the value of η ( n ) in the formula (15) converges to about 1.35 when n is large. Note also that the denominator in formula (16) converges to 2 ∗ Φ -1 (0.75) which is 1.34898 as n tends to infinity. When the sample size is small, our method will provide more accurate estimates than the formula (17) for the standard deviation estimation.

Simulation study for C 1

In this section, we conduct simulation studies to compare the performance of Hozo et al.’s method and our new method for estimating the sample standard deviation. Following Hozo et al.’s settings, we consider five different distributions: the normal distribution with mean μ = 50 and standard deviation σ = 17, the log-normal distribution with location parameter μ = 4 and scale parameter σ = 0.3, the beta distribution with shape parameters α = 9 and β = 4, the exponential distribution with rate parameter λ = 10, and the Weibull distribution with shape parameter k = 2 and scale parameter λ = 35. The graph of each of these distributions with the specified parameters is provided in Additional file 1 . In each simulation, we first randomly sample n observations and compute the true sample standard deviation using the whole sample. We then use the median, the minimum and maximum values of the sample to estimate the sample standard deviation by the formulas (6) and (9), respectively. To assess the accuracy of the two estimates, we define the relative error of each method as

With 1000 simulations, we report the average relative errors in Figure  1 for the normal distribution with the sample size ranging from 5 to 1001, and in Figure  2 for the four non-normal distributions with the sample size ranging from 5 to 101. For normal data which are most commonly assumed in meta-analysis, our new method provides a nearly unbiased estimate of the true sample standard deviation. Whereas for Hozo et al.’s method, we do observe that the best cutoff value is about n = 15 for switching between the estimates ( b - a ) / 12 and ( b - a )/4, and is about n = 70 for switching between ( b - a )/4 and ( b - a )/6. However, its overall performance is not satisfactory by noting that the estimate always fluctuates from -20% to 20% of the true sample standard deviation. In addition, we note that ξ (27)≈4 from Table  1 and ξ ( n )≈6 when Φ -1 (( n - 0.375)/( n + 0.25)) = 3, that is, n = (0.375 + 0.25 ∗ Φ (3))/(1 - Φ (3)) ≈ 463. This coincides with the simulation results in Figure  1 where the method ( b - a )/4 crosses the x -axis between n = 20 and n = 30, and the method ( b - a )/6 crosses the x -axis between n = 400 and n = 500.

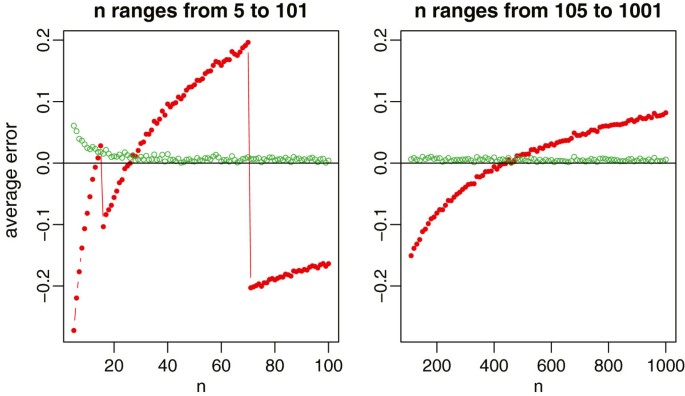
Relative errors of the sample standard deviation estimation for normal data, where the red lines with solid circles represent Hozo et al.’s method, and the green lines with empty circles represent the new method.

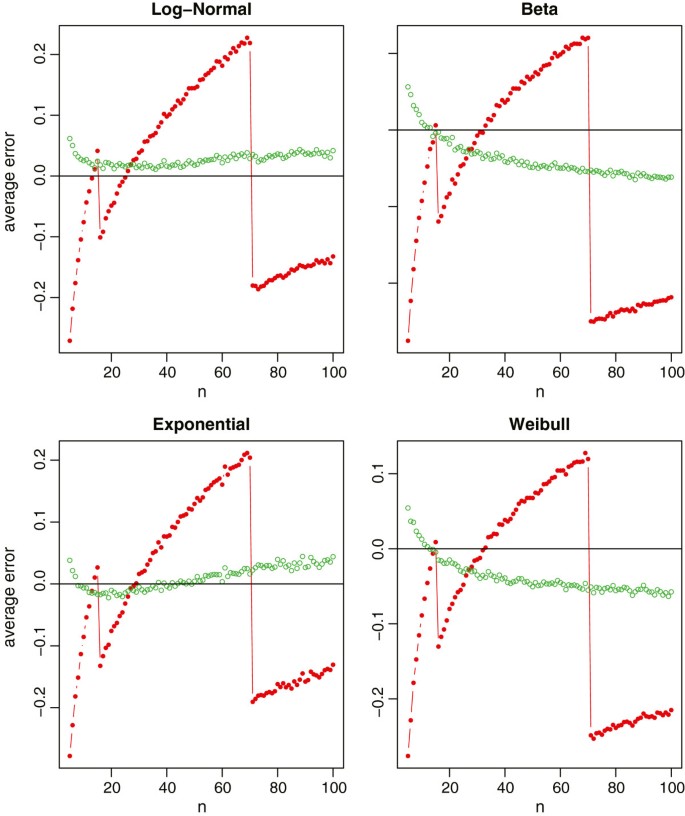
Relative errors of the sample standard deviation estimation for non-normal data (log-normal, beta, exponential and Weibull), where the red lines with solid circles represent Hozo et al.’s method, and the green lines with empty circles represent the new method.

From Figure  2 with the skewed data, our proposed method (9) makes a slightly biased estimate with the relative errors about 5% of the true sample standard deviation. Nevertheless, it is still obvious that the new method is much better compared to Hozo et al.’s method. We also note that, for the beta and Weibull distributions, the best cutoff values of n should be larger than 70 for switching between ( b - a )/4 and ( b - a )/6. This again coincides with Table one in Hozo et al. [ 3 ] where the suggested cutoff value is n = 100 for Beta and n = 110 for Weibull.

Simulation study for C 2

In this section, we evaluate the performance of the proposed method (13) and compare it to Bland’s method (11). Following Bland’s settings, we consider (i) the normal distribution with mean μ = 5 and standard deviation σ = 1, and (ii) the log-normal distribution with location parameter μ = 5 and scale parameter σ = 0.25, 0.5, and 1, respectively. For simplicity, we consider the sample size being n = Q + 1, where Q takes values from 1 to 50. As in Section 'Simulation study for C 1

’, we assess the accuracy of the two estimates by the relative error defined in (18).

In each simulation, we draw a total of n observations randomly from the given distribution and compute the true sample standard deviation of the sample. We then use and only use the minimum value, the first quartile, the median, the third quartile, and the maximum value to estimate the sample standard deviation by the formulas (11) and (13), respectively. With 1000 simulations, we report the average relative errors in Figure  3 for the four specified distributions. From Figure  3 , we observe that the new method provides a nearly unbiased estimate of the true sample standard deviation. Even for the very highly skewed log-normal data with σ =1, the relative error of the new method is also less than 10% for most sample sizes. On the contrary, Bland’s method is less satisfactory. As reported in [ 10 ], the formula (11) only works for a small range of sample sizes (In our simulations, the range is about from 20 to 40). When the sample size gets larger or the distribution is highly skewed, the sample standard deviations will be highly overestimated. Additionally, we note that the sample standard deviations will be seriously underestimated if n is very small. Overall, it is evident that the new method is better than Bland’s method in most settings.

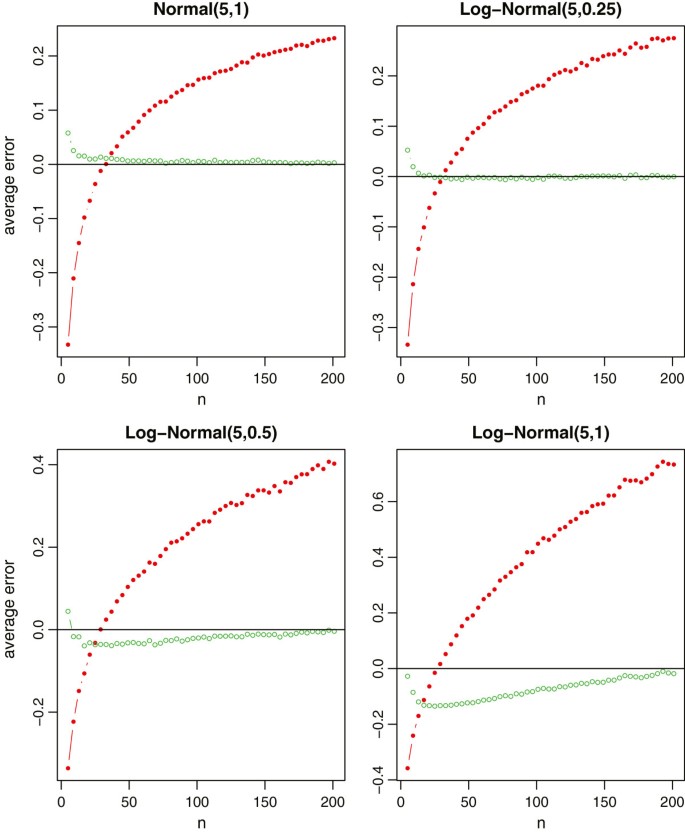
Relative errors of the sample standard deviation estimation for normal data and log-normal data, where the red lines with solid circles represent Bland’s method, and the green lines with empty circles represent the new method.

Simulation study for C 3

In the third simulation study, we conduct a comparison study that not only assesses the accuracy of the proposed method under Scenario C 3 , but also addresses a more realistic question in meta-analysis, “ For a clinical trial study, which summary statistics should be preferred to report, C 1 , C 2 or C 3 ? and why? "

For the sample mean estimation, we consider the formulas (3), (10), and (14) under three different scenarios, respectively. The accuracy of the mean estimation is also assessed by the relative error, which is defined in the same way as that for the sample standard deviation estimation. Similarly, for the sample standard deviation estimation, we consider the formulas (9), (13), and (15) under three different scenarios, respectively. The distributions we considered are the same as in Section 'Simulation study for C 1

’, i.e., the normal, log-normal, beta, exponential and Weibull distributions with the same parameters as those in previous two simulation studies.

In each simulation, we first draw a random sample of size n from each distribution. The true sample mean and the true sample standard deviation are computed using the whole sample. The summary statistics are also computed and categorized into Scenarios C 1 , C 2 and C 3 . We then use the aforementioned formulas to estimate the sample mean and standard deviation, respectively. The sample sizes are n = 4 Q + 1, where Q takes values from 1 to 50. With 1000 simulations, we report the average relative errors in Figure  4 for both X ̄ and S with the normal distribution, in Figure  5 for the sample mean estimation with the non-normal distributions, and in Figure  6 for the sample standard deviation estimation with the non-normal distributions.

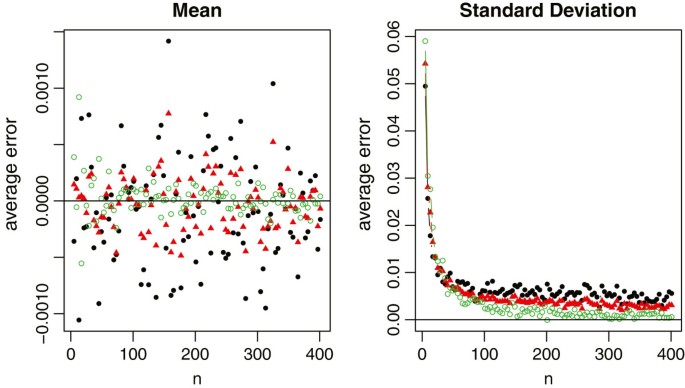
Relative errors of the sample mean and standard deviation estimations for normal data, where the black solid circles represent the method under scenario C 1 , the red solid triangles represent the method under scenario C 2 , and the green empty circles represent the method under scenario C 3 .

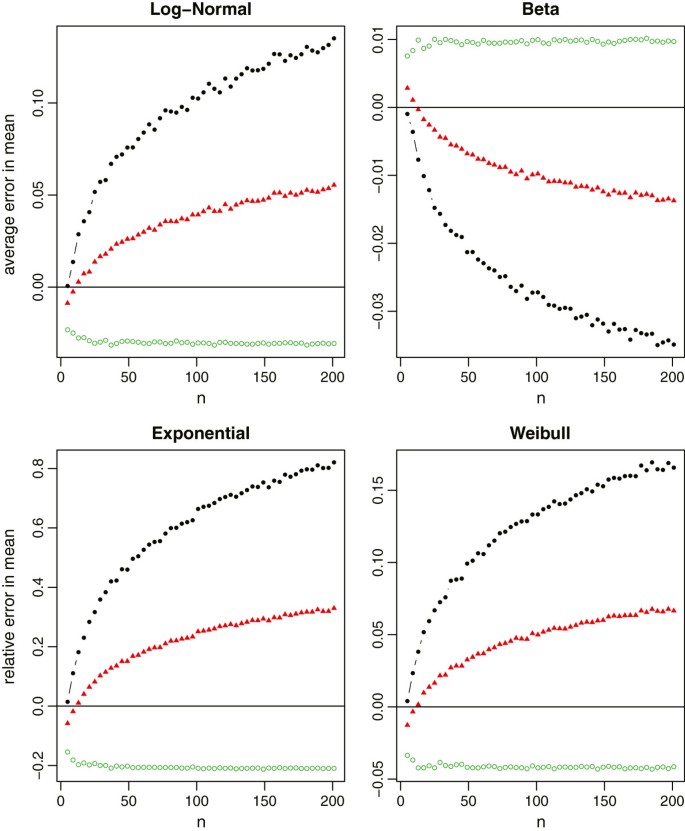
Relative errors of the sample mean estimation for non-normal data (log-normal, beta, exponential and Weibull), where the black lines with solid circles represent the method under scenario C 1 , the red lines with solid triangles represent the method under scenario C 2 , and the green lines with empty circles represent the method under scenario C 3 .

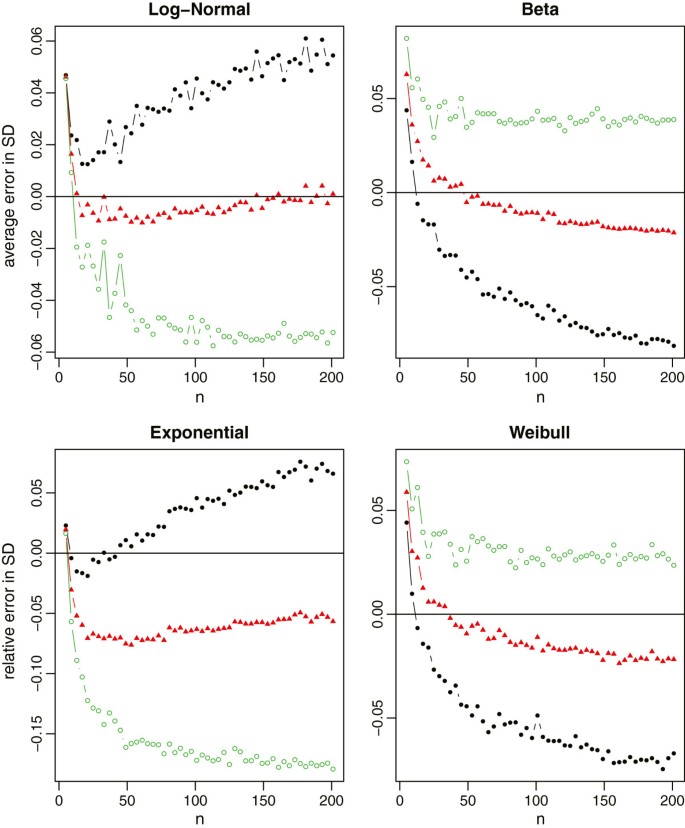
Relative errors of the sample standard deviation estimation for non-normal data (log-normal, beta, exponential and Weibull), where the black lines with solid circles represent the method under scenario C 1 , the red lines with solid triangles represent the method under scenario C 2 , and the green lines with empty circles represent the method under scenario C 3 .

For normal data which meta-analysis would commonly assume, all three methods provide a nearly unbiased estimate of the true sample mean. The relative errors in the sample standard deviation estimation are also very small in most settings (within 1% in general). Among the three methods, however, we recommend to estimate X ̄ and S using the summary statistics in Scenario C 3 . One main reason is because the first and third quartiles are usually less sensitive to outliers compared to the minimum and maximum values. Consequently, C 3 produces a more stable estimation than C 1 , and also C 2 that is partially affected by the minimum and maximum values.

For non-normal data from Figure  5 , we note that the mean estimation from C 2 is always better than that from C 1 . That is, if the additional information in the first and third quartiles is available, we should always use such information. On the other hand, the estimation from C 2 may not be consistently better than that from C 3 even though C 2 contains the additional information of minimum and maximum values. The reason is that this additional information may contain extreme values which may not be fully reliable and thus lead to worse estimation. Therefore, we need to be cautious when making the choice between C 2 and C 3 . It is also noteworthy that (i) the mean estimation from C 3 is not sensitive to the sample size, and (ii) C 1 and C 3 always lead to opposite estimations (one underestimates and the other overestimates the true value). While from Figure  6 , we observe that (i) the standard deviation estimation from C 3 is quite sensitive to the skewness of the data, (ii) C 1 and C 3 would also lead to the opposite estimations except for very small sample sizes, and (iii) C 2 turns out to be a good compromise for estimating the sample standard deviation. Taking both into account, we recommend to report Scenario C 2 in clinical trial studies. However, if we do not have all information in the 5-number summary and have to make a decision between C 1 and C 3 , we recommend C 1 for small sample sizes (say n ≤ 30), and C 3 for large sample sizes.

Researchers often use the sample mean and standard deviation to perform meta-analysis from clinical trials. However, sometimes, the reported results may only include the sample size, median, range and/or IQR. To combine these results in meta-analysis, we need to estimate the sample mean and standard deviation from them. In this paper, we first show the limitations of the existing works and then propose some new estimation methods. Here we summarize all discussed and proposed estimators under different scenarios in Table  3 .

We note that the proposed methods are established under the assumption that the data are normally distributed. In meta-analysis, however, the medians and quartiles are often reported when data do not follow a normal distribution. A natural question arises: “ To which extent it makes sense to apply methods that are based on a normal distribution assumption? ” In practice, if the entire sample or a large part of the sample is known, standard methods in statistics can be applied to estimate the skewness or even the density of the population. For the current study, however, the information provided is very limited, say for example, only a , m , b and n are given in Scenario 1. Under such situations, it may not be feasible to obtain a reliable estimate for the skewness unless we specify the underlying distribution for the population. Note that the underlying distribution is unlikely to be known in practice. Instead, if we arbitrarily choose a distribution (more likely to be misspecified), then the estimates from the wrong model can be even worse than that from the normal distribution assumption. As a compromise, we expect that the proposed formulas under the normal distribution assumption are among the best we can achieve.

Secondly, we note that even if the means and standard deviations can be satisfyingly estimated from the proposed formulas, it still remains a question to which extent it makes sense to use them in a meta-analysis, if the underlying distribution is very asymmetric and one must assume that they don’t represent location and dispersion adequately. Overall, this is a very practical yet challenging question and may warrant more research. In our future research, we propose to develop some test statistics (likelihood ratio test, score test, etc) for pre-testing the hypothesis that the distribution is symmetric (or normal) under the scenarios we considered in this article. The result of the pre-test will then suggest us whether or not we should still include the (very) asymmetric data in the meta-analysis. Other proposals that address this issue will also be considered in our future study.

Finally, to promote the usability, we have provided an Excel spread sheet to include all formulas in Table  3 in Additional file 2 . Specifically, in the Excel spread sheet, our proposed methods for estimating the sample mean and standard deviation can be applied by simply inputting the sample size, the median, the minimum and maximum values, and/or the first and third quartiles for the appropriate scenario. Furthermore, for ease of comparison, we have also included Hozo et al.’s method and Bland’s method in the Excel spread sheet.

In this paper, we discuss different approximation methods in the estimation of the sample mean and standard deviation and propose some new estimation methods to improve the existing literature. Through simulation studies, we demonstrate that the proposed methods greatly improve the existing methods and enrich the literature. Specifically, we point out that the widely accepted estimator of standard deviation proposed by Hozo et al. has some serious limitations and is always less satisfactory in practice because the estimator does not fully incorporate the sample size. As we explained in Section 'Estimating X ̄ and S from C 1 ’, using ( b - a )/6 for n > 70 in Hozo et al.’s adaptive estimation is untenable because the range b - a tends to be infinity as n approaches infinity if the distribution is not bounded, such as the normal and log-normal distributions. Our estimator replaces the adaptively selected thresholds ( 12 , 4 , 6 ) with a unified quantity 2 Φ -1 (( n - 0.375)/( n + 0.25)), which can be quickly computed and obviously is more stable and adaptive. In addition, our method removes the non-negative data assumption in Hozo et al.’s method and so is more applicable in practice.

Bland’s method extended Hozo et al.’s method by using the additional information in the IQR. Since extra information is included, it is expected that Bland’s estimators are superior to those in Hozo et al.’s method. However, the sample size is still not considered in Bland’s method for the sample standard deviation, which again limits its capability in real-world cases. Our simulation studies show that Bland’s estimator significantly overestimates the sample standard deviation when the sample size is large while seriously underestimating it when the sample size is small. Again, we incorporate the information of the sample size in the estimation of standard deviation via two unified quantities, 4 Φ -1 (( n - 0.375)/( n + 0.25)) and 4 Φ -1 ((0.75 n - 0.125)/( n + 0.25)). With some extra but trivial computing costs, our method makes significant improvement over Bland’s method when the IQR is available.

Moreover, we pay special attention to an overlooked scenario where the minimum and maximum values are not available. We show that the methodology following the ideas in Hozo et al.’s method and Bland’s method will lead to unbounded estimators and is not feasible. On the contrary, we extend the ideas of our proposed methods in the other two scenarios and again construct a simple but still valid estimator. After that, we take a step forward to compare the estimators of the sample mean and standard deviation under all three scenarios. For simplicity, we have only considered three most commonly used scenarios, including C 1 , C 2 and C 3 , in the current article. Our method, however, can be readily generalized to other scenarios, e.g., when only { a , q 1 , q 3 , b ; n } are known or when additional quantile information is given.

Antman EM, Lau J, Kupelnick B, Mosteller F, Chalmers TC: A comparison of results of meta-analyses of randomized control trials and recommendations of clinical experts: treatments for myocardial infarction. J Am Med Assoc. 1992, 268: 240-248. 10.1001/jama.1992.03490020088036.

Article   CAS   Google Scholar  

Cipriani A, Geddes J: Comparison of systematic and narrative reviews: the example of the atypical antipsychotics. Epidemiol Psichiatr Soc. 2003, 12: 146-153. 10.1017/S1121189X00002918.

Article   PubMed   Google Scholar  

Hozo SP, Djulbegovic B, Hozo I: Estimating the mean and variance from the median, range, and the size of a sample. BMC Med Res Methodol. 2005, 5: 13-10.1186/1471-2288-5-13.

Article   PubMed   PubMed Central   Google Scholar  

Triola M. F: Elementary Statistics, 11th Ed. 2009, Addison Wesley

Google Scholar  

Hogg RV, Craig AT: Introduction to Mathematical Statistics. 1995, Maxwell: Macmillan Canada,

David HA, Nagaraja HN: Order Statistics, 3rd Ed. 2003, Wiley Series in Probability and Statistics

Book   Google Scholar  

Blom G: Statistical Estimates and Transformed Beta Variables. 1958, New York: John Wiley and Sons, Inc.

Harter HL: Expected values of normal order statistics. Biometrika. 1961, 48: 151-165. 10.1093/biomet/48.1-2.151.

Article   Google Scholar  

Cramér H: Mathematical Methods of Statistics. 1999, Princeton University Press

Bland M: Estimating mean and standard deviation from the sample size, three quartiles, minimum, and maximum. International Journal of Statistics in Medical Research, in press. 2014,

Liu T, Li G, Li L, Korantzopoulos P: Association between c-reactive protein and recurrence of atrial fibrillation after successful electrical cardioversion: a meta-analysis. J Am Coll Cardiol. 2007, 49: 1642-1648. 10.1016/j.jacc.2006.12.042.

Article   CAS   PubMed   Google Scholar  

Zhu A, Ge D, Zhang J, Teng Y, Yuan C, Huang M, Adcock IM, Barnes PJ, Yao X: Sputum myeloperoxidase in chronic obstructive pulmonary disease. Eur J Med Res. 2014, 19: 12-10.1186/2047-783X-19-12.

Higgins JPT, Green S: Cochrane Handbook for Systematic Reviews of Interventions. 2008, Wiley Online Library

Pre-publication history

The pre-publication history for this paper can be accessed here: http://www.biomedcentral.com/1471-2288/14/135/prepub

Download references

Acknowledgements

The authors would like to thank the editor, the associate editor, and two reviewers for their helpful and constructive comments that greatly helped improving the final version of the article. X. Wan’s research was supported by the Hong Kong RGC grant HKBU12202114 and the Hong Kong Baptist University grant FRG2/13-14/005. T.J. Tong’s research was supported by the Hong Kong RGC grant HKBU202711 and the Hong Kong Baptist University grants FRG2/11-12/110, FRG1/13-14/018, and FRG2/13-14/062.

Author information

Authors and affiliations.

Department of Computer Science, Hong Kong Baptist University, Kowloon Tong, Hong Kong

Xiang Wan & Jiming Liu

Department of Statistics, Northwestern University, Evanston, IL, USA

Wenqian Wang

Department of Mathematics, Hong Kong Baptist University, Kowloon Tong, Hong Kong

Tiejun Tong

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Tiejun Tong .

Additional information

Competing interests.

The authors declare that they have no competing interests.

Authors’ contributions

TT, XW, and JL conceived and designed the methods. TT and WW conducted the implementation and experiments. All authors were involved in the manuscript preparation. All authors read and approved the final manuscript.

Xiang Wan, Wenqian Wang contributed equally to this work.

Electronic supplementary material

Additional file 1: the plot of each of those distributions in the simulation studies.(pdf 45 kb), additional file 2: an excel spread sheet including all formulas.(xlsx 11 kb), authors’ original submitted files for images.

Below are the links to the authors’ original submitted files for images.

Authors’ original file for figure 1

Authors’ original file for figure 2, authors’ original file for figure 3, authors’ original file for figure 4, authors’ original file for figure 5, authors’ original file for figure 6, rights and permissions.

Open Access  This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/ .

The Creative Commons Public Domain Dedication waiver ( https://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Wan, X., Wang, W., Liu, J. et al. Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range. BMC Med Res Methodol 14 , 135 (2014). https://doi.org/10.1186/1471-2288-14-135

Download citation

Received : 05 September 2014

Accepted : 12 December 2014

Published : 19 December 2014

DOI : https://doi.org/10.1186/1471-2288-14-135

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Interquartile range
• Meta-analysis
• Sample mean
• Sample size
• Standard deviation

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]